BOGOTA D.C
FECHA:21/02/2013
NOMBRES: Kaherine Yurani Talero Rodriguez, Jorge Armando Murcia Bedoya
SENA: Centro de Electricidad, Electrónica y Telecomunicaciones
AMBIENTE DE FORMACIÓN: 128 Alamos cra 89 A # 64C -33
INSTRUCTOR: Yaki Manuel Hortua
GRUPO:449622
PRUEBA DE POLARIDAD
La polaridad del transformador.
Como podremos imaginar, la polaridad del transformador dependerá de como están devanadas las dos bobinas, no solamente respecto al núcleo sino que también respecto entre ellas.
El punto negro representa la polaridad del transformador, algo que a lo mejor encontramos en los esquemas y, no necesariamente en la simbología general de diferentes tratados de electricidad y electrónica.
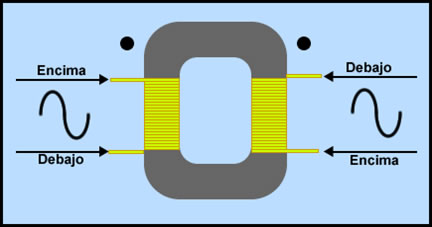
En el dibujo podemos observar la disposición de los devanados de las dos bobinas. En el mismo dibujo, observamos que al lado de las salidas de las bobinas, se indica por donde sale el final de la última espira y, por donde entra el principio de la primera espira. Es lo que podemos denominar el sentido de los devanados. Esto es muy importante para saber la polaridad del transformador. En este primer dibujo, tanto el voltaje de la bobina primaria y el voltaje de la bobina secundaria se encuentran en fase. Esto sucede porque el pico de tensión máximo de la bobina primaria coincide con el pico de tensión máximo de la bobina secundaria.
Nota : Como hemos indicado, el punto negro indica la polaridad. En el dibujo están dibujados en la parte de arriba del transformador, pero realmente daría lo mismo dibujar los dos puntos abajo, porque estamos ante un transformador en fase. La única exigencia es dibujar los puntos: o los dos arriba o los dos abajo, nunca en diagonal.
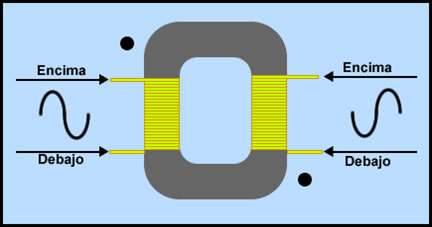
Por el contrario, en este otro dibujo, observamos como las bobinas han sido devanadas de diferente manera respecto a las bobinas del primer dibujo. En este caso, estamos tratando de un transformador desfasado 180°, y se dice que las bobinas tienen devanados con dirección opuesta.
Esto es así, porque el pico de tensión máxima de la bobina primaria esta desfasada 180° respecto al pico de tensión máxima de la bobina secundaria.
¿Qué es polaridad en un transformador?
Las bobinas secundarias de lostransformadores monofásicosse arrollan en el mismo sentido de la bobina primaria o en el sentido opuesto, según el criterio del fabricante.
Debido a esto, podría ser que la intensidad de corriente en la bobina primaria y la de la bobinasecundaria circulen en un mismo sentido, o en sentido opuesto.
Polaridad Aditiva:
La polaridad positiva se da cuando en un transformadorel bobinado secundario está arrollado en el mismo sentido que el bobinado primario.
Esto hace que los flujos de los dos bobinados giren en el mismo sentido y se sumen.
Los terminales “H1” y “X1” están cruzados.
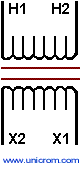
Polaridad Sustractiva:
La polaridad sustractiva se da cuando en un transformador el bobinado secundario esta arrollado en sentido opuesto al bobinado primario.
Esto hace que los flujos de los dos bobinados giren en sentidos opuestos y se resten.
Los terminales “H1” y “X1” están en línea.

Como determinar la polaridad de un transformador
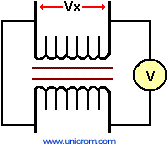 Para determinar la polaridad del transformador, se coloca un puente entre los terminales del lado izquierdo del transformador y se coloca un voltímetro entre los terminales del lado derecho del mismo, luego se alimenta del bobinado primario con un valor de voltaje (Vx).
Para determinar la polaridad del transformador, se coloca un puente entre los terminales del lado izquierdo del transformador y se coloca un voltímetro entre los terminales del lado derecho del mismo, luego se alimenta del bobinado primario con un valor de voltaje (Vx).
Si la lectura del voltímetro es mayor que Vx el transformador es aditivo o si es menor el transformador es sustractivo.
2) conexiones de los transformadores
CONEXIONES DE LOS TRANSFORMADORES TRÁFICOS


En nomenclatura abreviada se utilizan las letras mayúsculas para A.T. y
minúsculas para b.t.; para triángulo D, d; estrella Y, y; zigzag Z, z.
Según se realice la conexión de los devanados primario y secundario, se
obtendrán diferentes tipos de transformadores:
a) Estrella en el primario Y – estrella en el secundario y, o simplemente estrellaestrella Yy.
b) Estrella-triángulo Yd.
c) Estrella-zigzag Yz.
d) Triángulo-triángulo Dd.
e) Triángulo-estrella Dy.
Las relaciones de trasformación corresponden siempre a las ff.ee.mm. de vacío,
por lo que se utilizarán las nomenclaturas de V y E, indistintamente, para la tensión.
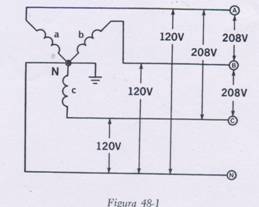
CONEXIÓN ESTRELLA-ESTRELLA.
En este tipo de transformador, sus devanados primarios y secundarios están
conectados en estrella, y se puede llevar el neutro tanto en el primario como en el
secundario.
La relación de transformación simple ms se determina como cociente entre el
número de espiras de una fase del primario y otra del secundario y coinciden con la
relación entre las ff.ee.mm. por fase de ambas en vacío:
La relación de transformación simple ms se determina como cociente entre el
número de espiras de una fase del primario y otra del secundario y coinciden con la
relación entre las ff.ee.mm. por fase de ambas en vacío:
La relación de transformación compuesta mc es el cociente entre las tensiones
de línea del primario al secundario, en vacío:
En la conexión estrella-estrella, se cumple: ms = mc.
El principal inconveniente de la conexión estrella-estrella es el desequilibrio de
tensiones en la línea conectada al primario, que aparece cuando fuertes desequilibrios
en la carga secundaria.
En el transformador estrella-estrella, con neutro en ambos devanados, al
sobrecargar una fase en el secundario Ia, aumentará proporcionalmente la corriente en
la fase en el secundario Ia, aumentará proporcionalmente la corriente en la fase del
devanado de la misma columna del primario IA y, por tanto, provocará caída de tensión
mayor en un conductor de línea que en los otros dos. Las corrientes Ia e IA se cierran
por el neutro y no por las otras fases.
Las conexiones utilizadas en la práctica están normalizadas en grupos de conexión. El grupo de conexión caracteriza las conexiones de los dos arrollamientos y el desfase entre las fuerzas electromotrices correspondientes a ambos arrollamientos. Cada grupo se identifica con una cifra o índice de conexión que multiplicada por 30º, da como resultado el desfase en retraso, que existe entre las tensiones del mismo genero (simples o compuestas) del secundario respecto al primario del transformador en cuestión.
Estudio de la transformación trifásica en conexión estrella-estrella (Yy) con arrollamiento terciario
La conexión estrella – estrella tiene la gran ventaja de disminuir la tensión por fase del transformador, pero presenta inconvenientes cuando las cargas no están equilibradas. Para eliminar estos inconvenientes se dispone de un arrollamiento terciario el cual esta conectado en triángulo y cerrado en cortocircuito sobre sí mismo. Las fuerzas magnetomotrices, primaria y secundaria, debidas a esta sobrecarga, se compensan en cada columna, con lo que desaparecen los flujos adicionales y, con ellos, los inconvenientes que resultaban de las cargas desequilibradas.
El devanado terciario puede utilizarse para suministrar cargas locales con la tensión más conveniente. Puede alimentar los circuitos de control y las instalaciones auxiliares en las estaciones transformadoras.

Fig12. Transformador trifásico en conexión estrella-estrella con devanado terciario
Estudio de la transformación trifásica en conexión triángulo estrella (Dy)
Existen cuatro formas de montaje con lo que respecta a la estrella secundaria:
- Desfase de 30º (Dy1).
- Desfase de 150º (Dy5).
- Desfase de -30º (Dy11).
- Desfase de -150º (Dy7).
De estos grupos de conexión se utilizan en la práctica el Dy5 y el Dy11. Este sistema de conexión es el más utilizado en los transformadores elevadores de principio de línea, es decir en los transformadores de central. En el caso de cargas desequilibradas no provoca la circulación de flujos magnéticos por el aire, ya que el desequilibrio se compensa magnéticamente en las tres columnas. Como se puede disponer de neutro en el secundario, es posible aplicar este sistema de conexión a transformadores de distribución para alimentación de redes de media y baja tensión con cuatro conductores.

Fig13- Transformador trifásico en conexión triángulo-estrella y desfase de 150º

Fig14. Reparto de las corrientes en los arrollamientos de un transformador trifásico en conexión triángulo estrella, con una carga desequilibrada
Existen cuatro posibilidades de conexión:
- Desfase de 30º (Yd1).
- Desfase de 150º (Yd5).
- Desfase de -30º (Yd11).
- Desfase de -150º (Yd7).
De estos grupos de conexión, el más utilizado en la práctica es el Yd5 y el Yd11. El empleo más frecuente y eficaz de este tipo de conexión es en los transformadores reductores para centrales, estaciones transformadoras y finales de línea conectando en estrella el lado de alta tensión y en triángulo el lado de baja tensión.
En lo que se refiere al funcionamiento con cargas desequilibradas, el desequilibrio de cargas secundarias, se transmite al primario en forma compensada para cada fase.

Fig15. Transformador trifásico en conexión estrella triángulo y desfase de 150º (grupo de conexión Yd5)
Para evitar el inconveniente de cargas desequilibradas se conecta el arrollamiento secundario en zigzag. Esta conexión consiste en hacer que la corriente circula por cada conductor activo del secundario, afecte siempre igual a dos fases primarias, estas corrientes se compensan mutuamente con las del secundario.
Designando arbitrariamente los terminales del primario y con respecto a estas designaciones el secundario ofrece cuatro posibilidades distintas de conexión, dos de ellas que proceden del neutro. Estos grupos de conexión son:
- Desfase de 30º (Yz1).
- Desfase de 150º (Yz5).
- Desfase de -30º (Yz11).
- Desfase de -150º (Yz7).
De estos grupos de conexión los más utilizados son el Yz5 y el Yz11. Este tipo de conexión se emplea para transformadores reductores de distribución, de potencia hasta 400KVA; para mayores potencias resulta más favorable el transformador conectado en triángulo estrella.

Fig16. Representación esquemática y diagrama vectorial de un transformador trifásico en conexión estrella zig-zag
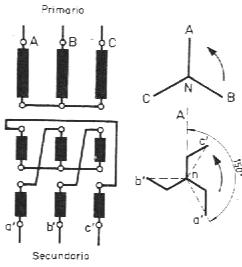
Fig17.- Transformador trifásico en conexión estrella zig-zag y desfase de 150º (grupo de conexión Yz5)
También ahora existen cuatro posibilidades de conexión que corresponden a las siguientes condiciones.
- a) los terminales de la red primaria y secundaria pueden ser homólogos o de opuesta polaridad
- b) la sucesión de estos terminales en el circuito interno puede ser la misma para ambos sistemas o inversa.
En la práctica se emplean solamente dos grupos de conexión que corresponden, respectivamente a un desfase de 0º y a un desfase de 180º.
Cada aislamiento debe soportar la tensión total de la línea correspondiente y, si la corriente es reducida, resulta un número elevado de espiras, de pequeña sección.
Si se interrumpe un arrollamiento, el transformador puede seguir funcionando aunque a potencia reducida, con la misma tensión compuesta y con una intensidad de línea a la que permite una sola fase. Se limita a transformadores de pequeña potencia para alimentación de redes de baja tensión, con corrientes de línea muy elevadas por la ausencia de neutro en ambos arrollamientos.

Fig18. Transformador trifásico en conexión triángulo-triángulo y desfase de 0º (grupo de conexión Dd0)

Fig19. Funcionamiento de un transformador trifásico en conexión triángulo-triángulo, con un arrollamiento interrumpido
Además de las conexiones estándar de los transformadores existen otras conexiones para lograr una transformación trifásica solamente con dos trasformadores:
Algunas de las más importantes son:
- Conexión
 abierta (o V-V)
abierta (o V-V) - Conexión en Y abierta -
 abierta
abierta - Conexión Scout-T
- Conexión trifásica en T
A continuación describiremos las características más importantes de cada una de estas conexiones.
Conexión abierta (o V-V)

Fig20..- Conexión  abierta (o V-V)
abierta (o V-V)
 abierta (o V-V)
abierta (o V-V)
Esta transformación puede utilizarse cuando por ejemplo en una conexión  de transformadores separados, una fase tiene una falla, la cual debe remitirse para ser reparada. Entonces:
de transformadores separados, una fase tiene una falla, la cual debe remitirse para ser reparada. Entonces:
 de transformadores separados, una fase tiene una falla, la cual debe remitirse para ser reparada. Entonces:
de transformadores separados, una fase tiene una falla, la cual debe remitirse para ser reparada. Entonces:
Si los dos voltajes secundarios que permanecen son:
Entonces esta quiere decir que a pesar de que se remueva una fase el sistema sigue manteniendo sus características primordiales
Aplicación de la conexión abierta
Es usada fundamentalmente para suministrar una pequeña cantidad de potencia trifásica a una carga monofásica, como se muestra en la siguiente figura:

Fig21. Aplicación de la conexión abierta
La conexión Y abierta –  delta abierta es muy similar a la conexión delta abierta con la única variante que los voltajes primarios se derivan de dos fases y el neutro. Su aplicación primordial es la de proveer de un sistema trifásico en donde solo existe la presencia de dos fases. La desventaja es este tipo de sistemas es que la corriente de retorno es muy grande y debe fluir por el neutro del ciercito primario.
delta abierta es muy similar a la conexión delta abierta con la única variante que los voltajes primarios se derivan de dos fases y el neutro. Su aplicación primordial es la de proveer de un sistema trifásico en donde solo existe la presencia de dos fases. La desventaja es este tipo de sistemas es que la corriente de retorno es muy grande y debe fluir por el neutro del ciercito primario.
 delta abierta es muy similar a la conexión delta abierta con la única variante que los voltajes primarios se derivan de dos fases y el neutro. Su aplicación primordial es la de proveer de un sistema trifásico en donde solo existe la presencia de dos fases. La desventaja es este tipo de sistemas es que la corriente de retorno es muy grande y debe fluir por el neutro del ciercito primario.
delta abierta es muy similar a la conexión delta abierta con la única variante que los voltajes primarios se derivan de dos fases y el neutro. Su aplicación primordial es la de proveer de un sistema trifásico en donde solo existe la presencia de dos fases. La desventaja es este tipo de sistemas es que la corriente de retorno es muy grande y debe fluir por el neutro del ciercito primario.
La conexión Scott-T es una forma de derivar de una fuente trifásica, dos fases desfasadas  La aplicación fundamental es producir la potencia necesaria para cubrir cualquier necesidad.
La aplicación fundamental es producir la potencia necesaria para cubrir cualquier necesidad.
 La aplicación fundamental es producir la potencia necesaria para cubrir cualquier necesidad.
La aplicación fundamental es producir la potencia necesaria para cubrir cualquier necesidad.
La conexión Scott-T consta de dos transformadores trifásicos de idénticas capacidades; uno de ellos tiene una toma en su devanado primario a 86.6% del valor del voltaje pleno. Esta toma se conecta a la toma central del otro transformador; los voltajes aplicados se colocan como se muestra la siguiente figura.

Fig22. Conexión Scott
Puesto que los voltajes están desfasados lo que se produce es un sistema bifásico. También con esta conexión es posible convertir potencia bifásica en potencia trifásica.
Esta conexión es una pequeña variante de la conexión Scott-T para convertir potencia trifásica en potencia trifásica pero a diferente nivel de voltaje. Esta conexión se nuestra en la figura siguiente.
Como en la conexión Scott-T los voltajes en los devanados primarios están desfasados  al igual que los voltajes secundarios con la única diferencia de las dos fases se recombinan para darnos un sistema trifásico. La ventaja de esta conexión con respecto a las demás conexiones con dos transformadores es que en esta se puede conectar el neutro tanto en los devanados primarios como secundarios.
al igual que los voltajes secundarios con la única diferencia de las dos fases se recombinan para darnos un sistema trifásico. La ventaja de esta conexión con respecto a las demás conexiones con dos transformadores es que en esta se puede conectar el neutro tanto en los devanados primarios como secundarios.
 al igual que los voltajes secundarios con la única diferencia de las dos fases se recombinan para darnos un sistema trifásico. La ventaja de esta conexión con respecto a las demás conexiones con dos transformadores es que en esta se puede conectar el neutro tanto en los devanados primarios como secundarios.
al igual que los voltajes secundarios con la única diferencia de las dos fases se recombinan para darnos un sistema trifásico. La ventaja de esta conexión con respecto a las demás conexiones con dos transformadores es que en esta se puede conectar el neutro tanto en los devanados primarios como secundarios.
Fig23. Conexión trifásica en T
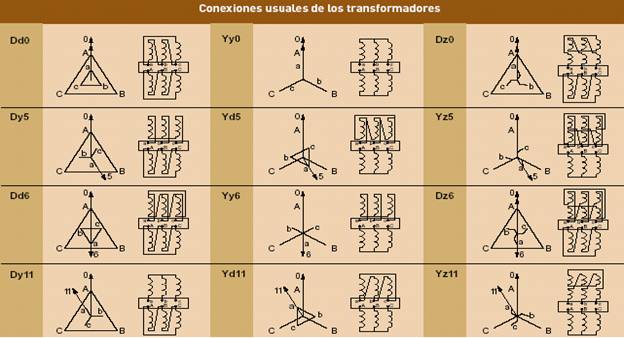
La conexión de los devanados trifásicos se designa con las letras Y, D y Z para los devanados de alta tensión e y, d, z para los de baja tensión (figura Nº 1.4). Si el punto neutro de los devanados en estrella o en zigzag es accesible para su conexión, las designaciones se convierten en YN o ZN e yn o zn.
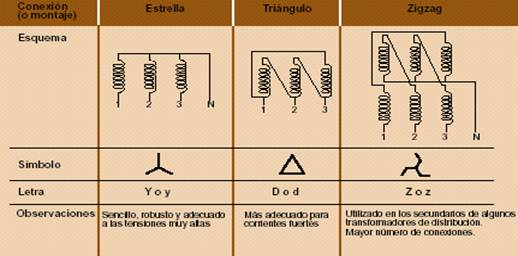
Figura Nº 1.4
• Estrella / Estrella (Y,y): Robusta, sencilla, neutra y accesible, pero inadecuada en régimen desequilibrado y con corrientes muy fuertes.
• Estrella / Triángulo (Y,d): Buen comportamiento en régimen desequilibrado y ausencia de armónicos de tercer orden, pero no es posible la distribución BT con cuatro hilos (no hay neutro en el secundario).
• Triángulo / Estrella (D,y): Sin neutro en el primario pero con posibilidad de neutro en el secundario (puesta a tierra y distribución con 4 hilos).
• Estrella / Zigzag (Y,z): Primario adecuado para AT (alta tensión), posibilidad de punto neutro puesto a tierra, ausencia de armónicos de tercer orden, buen comportamiento en régimen desequilibrado, caídas de tensión interna pequeñas pero mayor costo y volumen, y realización más delicada.
• Triángulo Zigzag (D,z): Similar calidad que la anterior, con mejor comportamiento en régimen desequilibrado pero sin neutro en el primario.
La designación de las conexiones (por medio de letras, figura Nº 1.5) se completa con una cifra que indica el desfase angular, por ejemplo Yy6, Yd11, Ynyn0 (neutro de salida). Donde esa cifra corresponde n*30°.
3) circuitos equivalentes de los ensayos del transformador y sus respectivas ecuaciones:
La Figura 1 muestra el circuito equivalente de un transformador de dos arrollamientos en el que sus lados primario y secundario están relacionados mediante la relación de transformación Np/Ns. Este circuito puede servir para representar un transformador monofásico o cualquiera de las fases de un transformador trifásico, tanto en régimen permanente como en procesos transitorios de baja frecuencia. En caso de tener que analizar el comportamiento completo de un transformador trifásico, además de incluir la representación de las tres fases, sería necesario tener en cuenta el tipo de conexión en ambos lados del transformador.
En este trabajo sólo se analizan circuitos adecuados para representar un transformador de dos arrollamientos funcionando en régimen permanente y en condiciones de carga simétrica y equilibrada. En tales condiciones, un transformador trifásico se puede representar mediante un circuito equivalente monofásico.
Figura 1. Circuito equivalente de un transformador con dos arrollamientos.
Los parámetros que aparecen en el circuito de la Figura 1 tienen un significado físico muy concreto:
- Rm y Lm son los parámetros del núcleo del transformador; Rm representa las pérdidas en el núcleo, mientras que Lm representa el flujo de magnetización confinado en el núcleo y común a los dos arrollamientos del transformador.
- Rp, Lp, Rs y Ls son los parámetros de los arrollamientos; Rp y Rs representan las pérdidas por efecto Joule de los dos arrollamientos del transformador, y Lp y Ls representan los flujos de dispersión de cada arrollamiento.
- La relación Np/Ns es la relación entre el número de espiras de los lados primario y secundario del transformador, o lo que es igual la relación de transformación entre tensiones y corrientes nominales de ambos lados.
La representación de la Figura 1 no es la única utilizada en estudios con transformadores. Es muy corriente el uso de circuitos equivalentes en los que los dos arrollamientos del transformador se representan mediante una sola resistencia y una sola inductancia, ya sea referida al lado primario
o al lado secundario. Por otro lado, los parámetros del núcleo, Rm y Lm, también podrían haber sido situados en el lado secundario. En todos los casos se ha supuesto que el parámetro Lm es no lineal. Una representación más rigurosa habría considerado que también es no lineal el parámetro Rm, y habría tenido en cuenta la dependencia de Rm con respecto a la frecuencia.
El circuito de la Figura 1 es utilizado en el cálculo de procesos transitorios de baja frecuencia y en determinados estudios en régimen permanente, aunque en este último caso se suele considerar que el parámetro Lm tiene un comportamiento lineal. Para determinados estudios, el circuito equivalente de un transformador se puede simplificar, prescindiendo de los parámetros que representan el núcleo. En este trabajo se supone que cualquiera de los circuitos de la Figura 2 representa el comportamiento de un transformador con suficiente precisión [6-7, 13-14]. De hecho en algún caso se prescindirá incluso del parámetro resistencia. Para obtener los parámetros de los circuitos de la Figura 2 será necesario conocer los valores obtenidos en el ensayo normalizado en cortocircuito.
Figura 2. Circuitos equivalentes simplificados de un transformador con dos arrollamientos.
Si se utilizan los siguientes símbolos:
- Potencia nominal Sn, en kVA o MVA
- Tensiones nominales Vn1, Vn2, en kV
- Tensión de cortocircuito εcc, (en pu o en %)
- Pérdidas por efecto Joule en el ensayo en cortocircuito Wcc, en kW o MW el cálculo de los parámetros del circuito equivalente simplificado y referido al secundario podría ser como sigue (Figura 2b):
 | (1a) |
 | (1b) |
| (1c) |
donde Z2 es la impedancia total de los arrollamientos, referida al lado secundario, y f es la frecuencia de operación del sistema en el que funciona el transformador.
Por lo que respecta al cálculo de parámetros referidos al lado primario (Figura 2a), sólo es necesario cambiar el subíndice "2" por el subíndice "1" en el símbolo de tensión nominal y aplicar el mismo proceso.
Los valores de resistencia, inductancia (o reactancia) e impedancia de los circuitos de la Figura 2 se conocen también como resistencia, inductancia (o reactancia) e impedancia de cortocircuito. Así, por tanto, en el resto del artículo se utilizarán los siguientes símbolos:
| (2a) | |
| (2b) |
En la aplicación de estas fórmulas se supone que los valores de εcc y Wcc, son los mismos independientemente de cuál sea el lado por el que se alimenta o el lado por el que se cortocircuita el transformador durante el ensayo en cortocircuito.
Circuito equivalente de un transformador con regulación
Este artículo presenta una metodología para la obtención y utilización del circuito equivalente de un transformador con regulación en el que es posible variar su relación de transformación. Este aspecto está insuficientemente tratado en la mayoría de libros de texto actuales en los que el circuito de un transformador con regulación se presenta de forma poco justificada. Este documento muestra cómo obtener el circuito equivalente del transformador y cómo aplicarlo utilizando tanto valores reales como valores por unidad (pu). El tratamiento con valores por unidad se puede realizar seleccionando los valores base de forma arbitraria, lo que supone una ventaja evidente cuando se trata de determinar alguna de las tensiones nominales del transformador en estudio. Aunque el objetivo del artículo es el de presentar un método para transformadores con regulación, el método es también válido para transformadores con relación de transformación constante en los que se tenga que determinar alguna de sus tensiones nominales. El artículo incluye dos ejemplos con campos de aplicación muy distintos que servirán para ilustrar las ventajas del método propuesto.
Palabras clave: Transformador de potencia, transformador con tomas, circuito equivalente, análisis en régimen permanente, modelación, valores por unidad.
El estudio se realizará con un transformador monofásico del que se conocen la potencia nominal (Sn), las tensiones nominales (Vn1, Vn2), la tensión de cortocircuito (εcc) y las pérdidas de potencia por efecto Joule obtenidas en el ensayo en cortocircuito (Wcc).
La relación entre los valores nominales de un transformador es:
| (3) |
Los valores base utilizados para obtener el circuito equivalente con parámetros por unidad se escogen inicialmente de forma arbitraria:
- Potencia base: Sb
- Tensiones base: Vb1, Vb2
De aquí se obtienen las siguientes intensidades e impedancias base:
 | (4a) |
 | (4b) |
El estudio se realiza suponiendo que ni la tensión aplicada en el ensayo de cortocircuito, εcc, generalmente expresada en valor porcentual (%) con respecto a las tensiones nominales, ni las pérdidas de potencia por efecto Joule medidas en el mismo ensayo, Wcc, dependen de la toma, o sea, de la relación de transformación en el transformador. De forma intuitiva es posible razonar que al cambiar la toma del transformador el flujo de dispersión en el lado de la toma varía de forma proporcional y que, por tanto, la tensión de cortocircuito referida a la nueva tensión nominal seguirá siendo la misma. Por lo que respecta a las pérdidas por efecto Joule, se puede suponer que al variar la toma o la tensión nominal en un lado del transformador, se modifican la resistencia y la intensidad de forma proporcional. Como las pérdidas dependen del cuadrado de la intensidad y la impedancia varía con el cuadrado de la relación de transformación, se puede suponer que ambos efectos se compensan cuando se juntan las pérdidas de los dos arrollamientos en una sola cantidad.
En realidad no es estrictamente correcto suponer que la tensión de cortocircuito de un transformador expresada en forma porcentual es independiente de la toma del transformador. Sin embargo, cuando se trata de obtener el circuito equivalente de un transformador con regulación, esta aproximación es utilizada en los libros de texto y en muchos estudios en los que la representación del transformador se deriva de alguno de los circuitos mostrados en la Figura 2.
La sección ha sido dividida en dos partes, en cada una de las cuales se obtendrá un circuito equivalente del transformador con regulación. Aplicando las hipótesis comentadas en el párrafo anterior, se puede concluir que el valor de la impedancia de cortocircuito de un transformador se puede obtener referida a su lado secundario cuando se conoce la tensión nominal de este lado y las tomas de regulación se sitúan en el lado primario, ver ecuaciones (1). Inversamente, será posible obtener la impedancia de cortocircuito referida al lado primario cuando las tomas de regulación se sitúan en el lado secundario y, por tanto, se conoce la tensión nominal del ladoprimario.
Impedancia de cortocircuito vista desde el lado secundario
La Figura 3 muestra el circuito equivalente de un transformador visto desde su lado secundario, en el que se puede regular su relación de transformación.
Las ecuaciones del circuito equivalente se pueden anotar de la siguiente forma:
 | (5) |
Donde
 | (6) |
El valor de Zcc2 se puede calcular cuando se conoce el valor de Vn2, tal como muestra la ecuación (6). Los valores de la resistencia, Rcc2, y la reactancia de cortocircuito, Xcc2, vistas desde el lado secundario, se calculan mediante las ecuaciones (1). En el estudio que se presenta a continuación se desconoce Vn1, y por tanto rt.
A partir de (5) se obtienen las siguientes ecuaciones de transmisión del transformador:
 | (7) |
En estas ecuaciones, la relación de transformación rt será desconocida, aunque en realidad la incógnita sea la tensión nominal de primario Vn1.
El objetivo es sintetizar un circuito pasivo a partir de estas ecuaciones de transmisión. La configuración del circuito será la que muestra la Figura 4.
Las ecuaciones de transmisión de este circuito son las siguientes:
 | (8) |
De la comparación entre las ecuaciones (7) y (8) se deduce que:
| (9) |
de donde se obtiene
 | (10) |
La Figura 5 muestra el circuito resultante, en el que rt suele ser una incógnita.
Figura 5. Circuito equivalente de un transformador visto desde el lado secundario.
La obtención del circuito equivalente con parámetros por unidad se puede realizar de varias formas. En este trabajo se realizará a partir de la ecuación (7), que puede expresarse en función de los valores base como sigue:
 | (11) |
donde Vb1, Vb2, Ib1 y Ib2 son los valores base de tensiones y corrientes, y  son los valores de tensiones y corrientes del transformador dados por unidad.
son los valores de tensiones y corrientes del transformador dados por unidad.
Nota: En este artículo los parámetros y variables (tensiones, corrientes y potencias) en valores por unidad se anotan con letras minúsculas, para diferenciarlos de los correspondientes valores expresados en cantidades físicas, que se anotan con letras mayúsculas.
La ecuación anterior queda de la siguiente forma:
 | (12) |
de donde resulta:
 | (13) |
siendo,
 | (14) |
Teniendo en cuenta la expresión de Zcc2, ver ecuación (6), el término  se puede escribir de la siguiente forma (nótese que se ha prescindido del carácter complejo de Zcc2).
se puede escribir de la siguiente forma (nótese que se ha prescindido del carácter complejo de Zcc2).
 | (15) |
de donde resulta:
 | (16) |
Puesto que el valor de la impedancia de cortocircuito por unidad vista desde el lado secundario es:
 | (17) |
resulta el siguiente sistema de ecuaciones con variables y parámetros por unidad:
 | (18) |
Haciendo,
| (19) |
queda finalmente:
 | (20) |
Siguiendo el mismo procedimiento que con los circuitos anteriores, el circuito al que corresponden estas ecuaciones puede ser cualquiera de los que muestra la Figura 6.
Figura 6. Circuito equivalente de un transformador con parámetros en pu visto desde el lado secundario.
El circuito de la Figura 6b es el que se suele analizar en la mayoría de textos cuando el objetivo del estudio es determinar la toma con la que debe operar un transformador para conseguir una determinada tensión en un nudo de la red en estudio.
Impedancia de cortocircuito vista desde el lado primario
La Figura 7 muestra el circuito equivalente de un transformador con regulación visto desde su lado primario
Figura 7. Circuito equivalente de un transformador visto desde el lado primario.
Las ecuaciones del circuito equivalente se pueden anotar de la siguiente forma:
 | (21) |
donde:
 | (22) |
A partir de (21) se obtienen las siguientes ecuaciones de transmisión:
 | (23) |
Siguiendo el mismo procedimiento que con el circuito anterior se obtiene el circuito de la Figura 8, en el que nuevamente la relación de transformación rt será una incógnita. En este caso la incógnita realmente es Vn2, ya que Vn1 es conocida y se utiliza para obtener Zcc1.
Figura 8. Circuito equivalente de un transformador visto desde el lado primario.
Las ecuaciones resultantes del circuito con parámetros por unidad son las siguientes:
 | (24) |
con
 | (25) |
El circuito al que corresponden estas ecuaciones puede ser cualquiera de los que muestra la Figura 9 si se sigue el mismo procedimiento que se empleó cuando los parámetros eran reales.
Figura 9. Circuito equivalente de un transformador con parámetros en pu visto desde el lado
El circuito de la Figura 9b es utilizado en muy pocos textos, ver por ejemplo [6].
Se puede demostrar que los parámetros del circuito de la Figura 6b y los del circuito de la Figura 9b son los mismos cuando el valor de a es conocido. Por ejemplo, para el parámetro central de ambos circuitos se tiene:
• Circuito equivalente Figura 6b
 | (26a) |
• Circuito equivalente Figura 9b
 | (26b) |
Es decir, cuando los valores base y los valores nominales son conocidos, independientemente del valor de a, el estudio se puede hacer con uno u otro circuito, ver Ejemplo 2. Sin embargo, esto no significa que se pueda utilizar uno u otro circuito indistintamente cuando se trata de calcular el valor de a, como se muestra en el Ejemplo 1. El circuito de la Figura 6b es el que debe utilizarse cuando se conoce la tensión nominal de secundario, y el de la Figura 9b cuando se conoce la tensión nominal de primario.
Otros circuitos equivalentes
Los circuitos anteriores fueron obtenidos con valores base escogidos de forma arbitraria. Sin embargo, si la selección de los valores base se realiza siguiendo determinados criterios es posible obtener otros circuitos equivalentes, según se indica a continuación.
1. Si rt = rb, resulta a = 1, y las ecuaciones (20) y (24) quedan, respectivamente:
 | (27a) |
 | (27b) |
Puesto que se ha supuesto que:
 | (28) |
también se cumple:
 | (29) |
on lo que a partir de (17) y (25), o (27), resulta
| (30) |
- muestra los resultados obtenidos a otro circuito produce los mismos resultados cuando partir de la expresión anterior con algunos de los el valor de a es conocido.
Nota: En todos los cálculos Vb1=13,8kV; Vb2=4,16kV; Sn = 10 MVA.
.
http://www.scielo.cl/scielo.php?pid=S0718-33052011000100010&script=sci_arttext
EJERCICIO N°1 DE TRANSFORMADORES
Un transformador que trabaja a una frecuencia de 50 Hz. Con unas chapa magnética de una
inducción de 1,2 Tesla (12000 Gauss), conectado a una red de 50 Hz. De frecuencia. El peso del
núcleo del transformador es de 3 kg. ¿Cuáles serán las perdidas por histéresis del núcleo
magnético?.
Formula de Steinmetz
Kh = Coeficiente de cada material = 0,002
F = frecuencia en Hz.
βmax = Inducción máxima en Tesla
Ph = perdidas por histéresis en Watios/Kg.
n = 1,6 si Βmax < 1 Tesla (10000 Gauss)
n = 2 si Βmax > 1 Tesla (10000 Gauss)
Ph = Kh * f * (βmax)
n
Ph = 0,002 * 50 * 1,2
2
Ph = 0,144 watios/kg
0,144 watios 1 kg
X 3 kg
X = 3 * 0,144 watios
X = 0,432 watios
EJERCICIO N°2 DE TRANSFORMADORES
EJERCICIO N°2 DE TRANSFORMADORES
Un transformador conectado a una red de 50 Hz. De frecuencia con una chapa magnética de 0,9
Tesla (9000 Gauss) de inducción. El peso del núcleo del transformador es de 12 kg. El espesor de la
chapa del núcleo es de 0,35 mm y el coeficiente de histéresis es de 0,002
Calcular la potencia perdida en el hierro?
Se halla la potencia perdida por corrientes de Foucault
Pf
= perdidas por corriente de Foucault en Watios/Kg.
F = frecuencia en Hz. = 50 Hz.
3βmaz = Inducción máxima en Gauss = 900 Gauss
Δ = Espesor de la chapa en mm. = 0,35 mm
v = volumen del nucleo
Las perdidas totales por corrientes de Foucault son:
0,545 watios 1 kg
X 12 kg
X = 12 * 0,545 watios
X = 6,54 watios
Se halla la potencia perdida por histéresis
Formula de Steinmetz
Kh = Coeficiente de cada material = 0,002
F = frecuencia en Hz. = 50 Hz
βmax = Inducción máxima en Tesla = 0,9 Tesla
Ph = perdidas por histéresis en Watios/Kg.
n = 1,6 si Βmax < 1 Tesla (10000 Gauss)
n = 2 si Βmax > 1 Tesla (10000 Gauss)
Ph = Kh * f * (βmax)
n
Ph = 0,002 * 50 * (0,9)
1,6
Ph = 0,002 * 50 * 0,84486
Ph = 0,0844 watios/kg
Las perdidas totales por histéresis son:
0,0844 watios 1 kg
X 12 kg
X = 12 * 0,0844 watios
X = 1,01 watios
Perdidas totales en el núcleo son:
PFE = perdidas totales por corrientes de Foucault + perdidas totales por histéresis
PFE = 6,54 watios + 1,01 watios
PFE = 7,55 watios
Nota: Las pérdidas en el hierro se halla midiendo la potencia consumida por el transformador en
vacío.
EJERCICIO N° 3 DE TRANSFORMADORES
Un transformador monofásico de 100 Kva. 3000/220 v, 50 Hz, tiene 100 espiras en el devanado
secundario. Supuesto que el transformador es ideal, calcular:
a) Corrientes primaria y secundaria a plena carga?
b) Flujo máximo
c) Numero de espiras del arrollamiento primario?
a) Los valores de la corriente primaria y secundaria a plena carga son:
S = 100 Kva = 100000 va
E1 = 3000 v
E2 = 220 V
I1 = Corriente del primario en amperios
I2 = Corriente del secundario en amperios
Un transformador monofásico de 100 Kva. 3000/220 v, 50 Hz, tiene 100 espiras en el devanado
secundario. Supuesto que el transformador es ideal, calcular:
a) Corrientes primaria y secundaria a plena carga?
b) Flujo máximo
c) Numero de espiras del arrollamiento primario?
a) Los valores de la corriente primaria y secundaria a plena carga son:
S = 100 Kva = 100000 va
E1 = 3000 v
E2 = 220 V
I1 = Corriente del primario en amperios
I2 = Corriente del secundario en amperios
Flujo máximo, como el transformador es ideal
N2 = 100 espiras en el secundario
F = 50 Hz
E2 = 220 V
Numero de espiras del arrollamiento primario?
N2 = 100 espiras en el secundario
E1 = 3000 v
E2 = 220 V
http://e-ducativa.catedu.es/44700165/aula/archivos/repositorio//3000/3015/html/134_valores_y_parmetros_de_un_transformador
VALORES Y PARÁMETROS DE UN TRANSFORMADOR
Para concluir este apartado es interesante conocer algunos de los parámetros que nos indican las características de los transformadores. Muchos de ellos son suministrados por el fabricante.
Algunos ya nos son conocidos, pues hemos hablado de ellos, tal es el caso de la relación de transformación, las resistencias y reactancias de primario y secundario, pero otros aún no los hemos citado.
RENDIMIENTO DE UN TRANSFORMADOR
si una maquina eléctrica cuyo objeto es cambiar las condiciones de Energía Eléctrica, concretamente en su tensión, para adecuarla a su utiliza o transporte. Esta formado por un circuito magnético de hierro y dos bobinas, una el primario, y la otra el secundario.
En el primario se conecta una fuente de tensión alterna U1, circulando a través de las N1 espiras del primario una corriente I1. Esta corriente variable produce un campo eléctrico variable, ya que b= f(I), en los conductores de la bobina. El flujo de este campo magnético variable circula por el circuito magnético. Por la Ley de Faraday la variación de campo magnético produce una tensión inducida en el segundario. Esto es:
Donde m es la relación de transformación.
Los datos de placa de un transformador suelen ser la potencia aparente, la tensión del primario y del secundario, y la tensión de cortocircuito en tanto por ciento. El rendimiento de un transformador viene dado por:
Las perdidas en el hierro son constantes respecto al índice de carga, y las perdidas en el cobre forma una parábola respecto al mismo índice. El rendimiento máximo del un transformador se produce cuando las perdidas en el hierro son iguales a las perdidas en el cobre. El rendimiento máximo se consigue para cargas como:
Existe un factor de carga (C) para el cual el redimiendo del transformador es máximo, y esto corresponde a 2/3, es decir, seleccionaremos un transformador cuyo punto de trabajo previsto para nuestra instalación sea el 66% de la potencia nominal del transformador:
http://www.unicrom.com/topic.asp?TOPIC_ID=7094&FORUM_ID=19&CAT_ID=8&Forum_Title=Noticias+y+Novedades+del+Sitio&Topic_Title=C%E1lculo+del+rendimiento+de+un+transformador
Rendimiento de un transformador
El rendimiento de un transformador se define como la relación entre la potencia de salida y la potencia absorbida de la red por el transformador

Para determinar el rendimiento de un transformador de una madera rápida y directa podemos medir con un vatímetro la potencia del bobinado primario y de igual forma con otro vatímetro la potencia del bobinado secundario, de tal forma que el rendimiento del transformador vendrá determinado por el coeficiente que resulte entre estos dos
Otra manera de calcular la eficiencia en un transformador es determinado el cociente de la potencia de salida y la potencia de entrada, sumándole las perdidas en el cobre y en el hierro



En la figura siguiente vemos la curva del rendimiento de un transformador con diferentes cargas y cos fi:

En la tabla siguiente vemos valores típicos de diferentes transformadores

CIBERGRAFIA
http://endrino.pntic.mec.es/jhem0027/eltrafotrifasico/eltrafotrifasico.htm
http://www.mcgraw-hill.es/bcv/guide/capitulo/8448141784.pdf


















